Mathematics
I recieved my PhD in mathematics at the University of Colorado Boulder under David Grant.
My mathematical interests are in arithmetic geometry. More specifically, I study elliptic curves, genus-two curves, abelian surfaces, curves of higher genus, higher-dimensional abelian varieties, p-adic numbers, theta functions, and modular forms.
Papersp-Adic Numbers
For each prime integer p, there is a whole set of numbers, alternative to the real numbers, which are well-suited to a version of calculus that somehow still remembers discrete properties around p.
Elliptic Curves
Elliptic curves are geometric objects with profound connections to many areas of mathematics.
Modular Forms
Modular forms are a certain class of geometric function. As complex functions, they encode classifying information about elliptic curves. At the same time, their power series coefficients exibit deep patterns in the integers.
Higher Genus Curves
Elliptic curves are just the start of the theory of algebraic curves, being the curves of genus one. Their higher-genus cousins form a furtile playground in which to enrich our understanding of everything we know from elliptic curves.
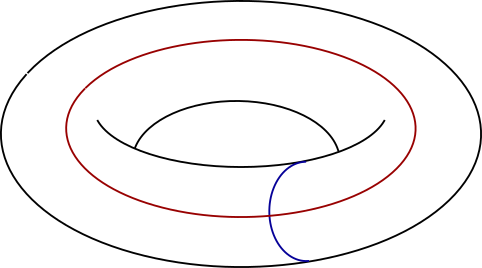
Abelian Varieties
Abelian varieties are yet another way to extend the essence of elliptic curves, but as geometric spaces of higher dimension.
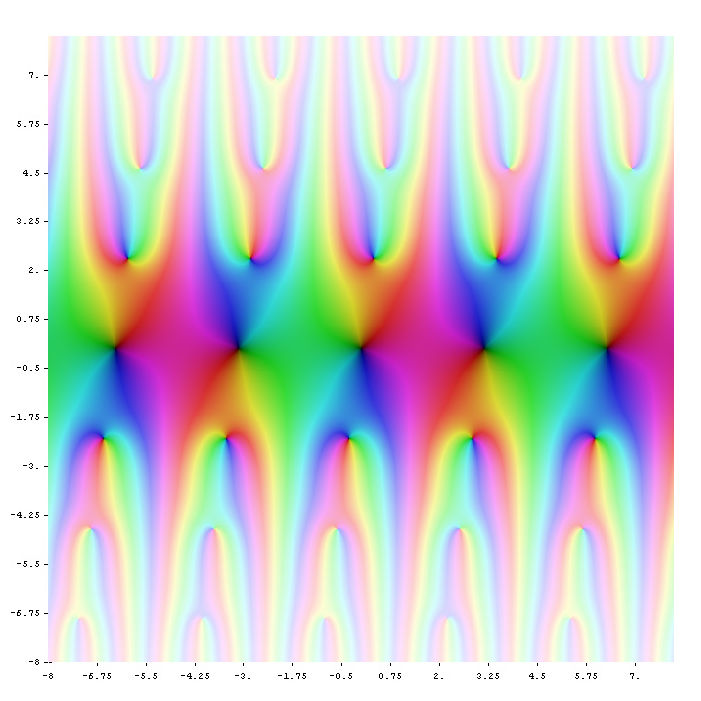
Theta Functions
Theta functions are a class of geometric function that encode some of both the modular information of modular forms and the geometric information of abelian varieties.
Papers
A collection of my papers are listed below:
| Title | Coauthors | Link |
|---|---|---|
| Twisted Kronecker theta functions and p-adic interpolation | Y. Choie | Submitted |
| Twisted Kronecker series and periods of modular forms on $\Gamma_0(\mathbb{N})$ | Y. Choie | Submitted |
| Universal p-adic sigma and Weierstrass zeta functions | D. Grant | Journal arXiv |
| Perfectoid covers of abelian varieties | D. Gvirtz, B. Heuer, D. Shchedrina, K. Shimizu, P. Wear, Z. Yao | Journal arXiv |
| Constants in Titchmarsh divisor problems for elliptic curves | R. Bell, A.C. Cojocaru, A. Cowan, N. Jones, V. Matei, G. Smith, I. Vogt | Journal arXiv |
| On Generalizations of p-Adic Weierstrass Sigma and Zeta Functions | self | Thesis |